코딩로그
[대학수학] 초월함수 본문
[초월함수]
- 삼각비
- 직각삼각형의 각과 변의 길이를 이용해 정의
- θ == 각
- θ는 호도법으로 표현, 1 라디안(radian)은 180˚ / π
- 180˚ == π
- 90˚ == π / 2
- 60˚ == π / 3


- 삼각함수
삼각함수
- 중심이 원점이고 반지름이 r인 원 위의 점 P(x, y)에 대하여 x축의 양의 부분을 시초점으로 하여
동경 OP가 나타내는 각의 크기를 θ라고 하면 각 θ는 y / r, x / r, y / x와 대응
이와 같이 각 θ와 대응되는 함수를 각각 sinθ, cosθ, tanθ라고 하며 다음과 같다
- sinθ = y / r
- cosθ = x / r
- tanθ = y / x (단, x != 0)
- sinθ의 역수 == cosecθ == r / y
- cosθ의 역수 == secθ == r / x
- tanθ의 역수 == cotθ == x / y- 삼각함수의 제곱 공식
- sinx와 cosx
- sin²x + cos²x = 1
- sinx와 cosx
- 삼각함수를 각도 θ의 함수가 아닌 일반적인 함수 y = f(x) 형태로 표시 → 주기함수
- y = sinx
- y = cosx
- y = tanx
- 주기함수
- 어떤 정수 n에 대해서 sinx = sin(x + 2nπ), cosx = cos(x + 2nπ)가 성립
- sin 함수와 cos 함수는 주기가 2π인 주기함수
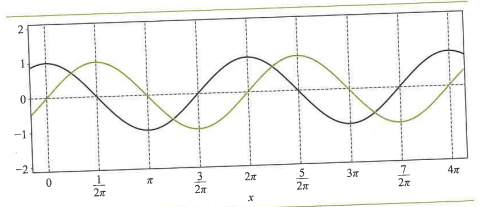
- 주기함수
- 어떤 정수 n에 대해서 tanx = tan(x + nπ)가 성립
- tan 함수는 주기가 π인 주기함수

주기함수
- 함수 f의 정의역에서 덧셈이 정의되어 있고 f(x)가 모든 정의역에 대해 f(x) = f(x+p)를 만족하는
0이 아닌 상수 p가 존재할 때 f(x)
- 삼각함수의 성질(sinx, cosx)
- sin(-x) == -sinx
- cos(-x) == cosx
- sin(x + π / 2) == cosx
- cos(x + π / 2) == -sinx
- sin(x + π) == -sinx
- cos(x + π) == -cosx
- 삼각함수의 성질(tanx)
- tan(-x) == -tanx
- tan(x + π / 2) == -cotx
- tan(x + π) == tan(x)
- 일반적인 sin함수
- y = Asin(ωx + ф)으로 표현
- 주기 → 2π / ω, 주기 함수가 얼마나 빠르게 반복되는가
- 주파수 → ω, 주기 함수가 얼마나 빠르게 반복되는가
- 진폭 → |A|, 파동의 크기
- 위상각(phase) → ф, sin 함수의 시작점

- 지수법칙
- 어떤 양수 a를 n번 거듭제곱 → aⁿ
- a → 밑
- ⁿ → 지수
- n을 실수 x로 확장하면 aˣ로 표현
- 어떤 양수 a를 n번 거듭제곱 → aⁿ
지수법칙
- 양수 a, b와 실수 x, y에 대하여 다음이 성립
1. a^(x+y) == a^x * a^y
2. a^(x-y) == a^x / a^y
3. (a^x)^y == a^xy
4. (ab)^x == a^x * b^x
5. x√a == a^(1/x)
- 지수함수
- a가 양의 상수일 때 정의역이 실수인 함수
- exponential function
- y = aˣ
- 치역 → 양의 실수
- 지수함수의 a값 → 무리수인 e = 2.71828...이 자주 사용
- e → 오일러의 수
- y == eˣ == exp(x)
- a의 값에 따라 모양이 변함
- 0 < a < 1
- x가 커짐에 따라 값이 작아짐
- a > 1
- x가 커짐에 따라 값이 커짐
- 0 < a < 1

- 로그함수
- 지수함수의 역함수 == 자연로그함수
- y == logₑx == ln x
- 지수함수가 y = 10ˣ일 때, y = logx → 밑이 10인 상용로그함수
로그함수
- 지수함수 f(x) = exp x의 역함수
- f^(-1)(x) = lnx
- exp(lnx) = x, 단 x > 0, ln(exp x) = x- 지수함수의 성질
- exp(x+y) = exp x * exp y
- exp(lnx + lny) = exp(lnx) * exp(lny) = xy = exp(lnxy)
- exp(lnx - lny) = exp(lnx) / exp(lny) = x / y = exp(lnx/y)
- exp(x+y) = exp x * exp y
- 로그함수의 성질
- ln(xy) = lnx + lny
- ln(x/y) = lnx - lny

'YJ > 대학수학' 카테고리의 다른 글
| [대학수학] 급수 (0) | 2022.09.16 |
|---|---|
| [대학수학] 수열의 극한 (0) | 2022.09.15 |
| [대학수학] 여러 가지 함수 (1) | 2022.09.08 |
| [대학수학] 함수의 연산 (0) | 2022.09.07 |
| [대학수학] 전단사함수와 역함수 (0) | 2022.09.07 |




